Ask The Experts: Sediment Transport Modeling

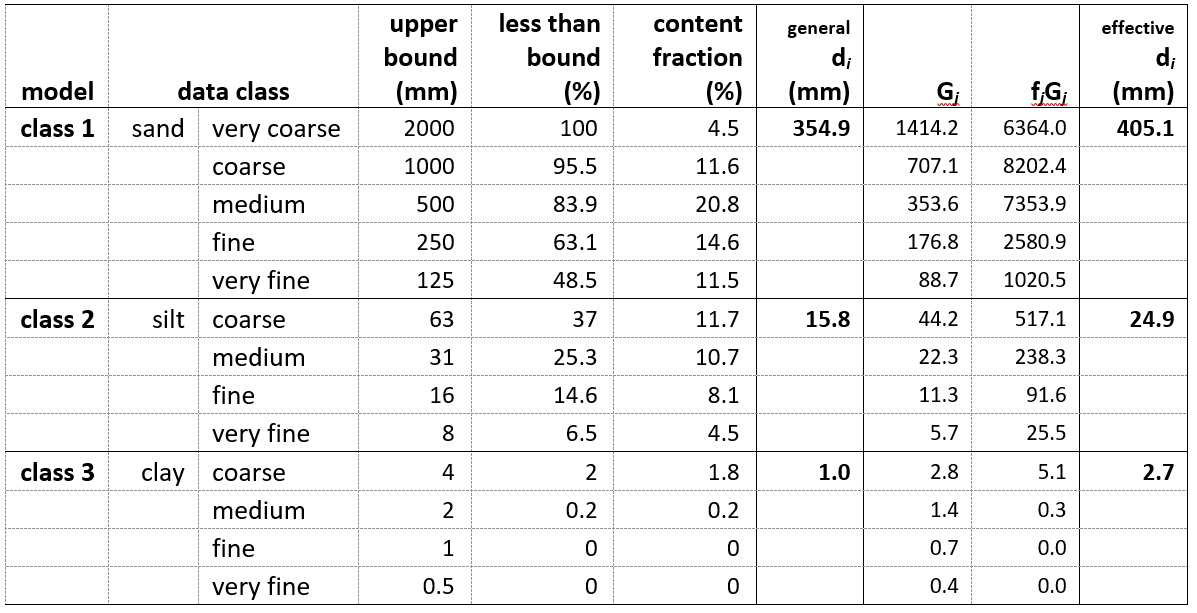
For sediment transport modeling, EFDC requires a modeler to define particle size classes and specify the median diameter for each class, which can represent the average behavior of the particles. A general approach to specify the median grain size for a modeling class $i$ is

$d_i = \exp \left[ \frac{\ln(\text{max}_i) + \ln(\text{min}_i)}{2} \right]$

where the $max_i$ and $min_i$ represent the upper and lower bounds of a modeling size class $i$, respectively.

Another approach uses an effective grain size for each modeling class based on the content fraction given data classes. For each modeling class $i$, the effective grain size $d_i$ can be computed as

$d*i = \frac{\sum*{j=1}^{n} f*j G_j}{\sum*{j=1}^{n} f_j}$

Where $f_j$ is fractional content of data class $j$, $G_j$ is geometric mean diameter for data class $j$, and $n$ is the number of data classes within a modeling size class $i$. This approach would be a better way when the high-resolution grain size distribution is available for given sediment data. Below table presents the median grain sizes for modeling size classes using example sediment data, and two approaches show different $d_i$ values over the classes.