Incorporation of COARE 3.6 into EFDC+

The Coupled Ocean-Atmosphere Response Experiment (COARE) bulk algorithm, developed by C. Fairall, E. F. Bradley, and D. Rogers, has become one of the most frequently used algorithms in the air-sea interaction community (Fairall et al., 1994; Fairall et al., 2003). The algorithm follows the standard Monin-Obukhov similarity theory (MOST) for near-surface meteorological measurements. It is designed to give estimates of the turbulent fluxes of sensible and latent heat and the stress from inputs of bulk variables. With release of EEMS 12.1, the Environmental Fluid Dynamics Code Plus (EFDC+) will offer a modeling feature to simulate these fluxes by incorporating the COARE subroutines. In this blog, we introduce the implementation of COARE into the EFDC+ code, as well as the updating of the EFDC+ Explorer graphical user interface for this feature.

Background Theory

Bulk algorithms to estimate surface fluxes are widely used in numerical models and applications where highly detailed local information is unavailable. These are based upon MOST representations of the fluxes in terms of mean quantities:

In equation 1, $w'x'$ shows the turbulent flux where $x$ is a variable that can be the wind component, the potential temperature, the water vapor specific humidity, etc and $w$is the vertical velocity. Here $C_x$ is the bulk transfer coefficient for the variable $x$ and $C_x$ is the total transfer coefficient. $ΔX$ is the air-sea difference in the mean value of $x$ and $S$ is the mean wind speed.

As a result of equation 1, the turbulent fluxes of stress component $Ï„$ sensible heat $H_s$ and latent heat $H_l$ are defined by the normal Reynolds averages,

Where $C*d$, $C_h$ and $C_e$ are the transfer coefficients for stress, sensible heat, and latent heat, respectively; $u_i$ is one of the horizontal wind components, $\theta$ is the potential temperature, and $q$ is the water vapor mixing ratio. $S$ is the average value of the wind speed and $\rho_a$ is the air density; $C*{pa}$ is the specific heat and $L*e$ is the latent heat of vaporization $u*{si}$ is the surface current; $T_s$ is the water surface temperature; and $q_s$ is the interfacial value of the water vapor mixing ratio. It is noted that the transfer coefficients in Equations (2), (3), and (4) have a dependence on surface stability prescribed by MOST.

The water surface is characterized by the velocity roughness, specified as Charnock’s expression, plus a smooth flow limit,

Where $u_∗$ is the friction velocity, and $\nu$is the water kinetic viscosity.

Implementation of COARE 3.6 into EFDC+

COARE Fortran subroutine (v3.6) has been implemented into the EFDC+ code to compute the bulk fluxes. The code source is available in the GitHub repository created by the NOAA/OAR/ESRL Physical Sciences Laboratory. Some modifications have been made to avoid the “divide by zero” error when evaluating the Monin-Obukhov length scale when running models. Additionally, a minimum value of 0.011 is assigned to the Charnock parameter to avoid a negative value estimated when the wind speed is lower than 2.94 m/s.

The COARE subroutine is called inside the EFDC+ heat module as a new option for the calculation of water surface heat exchange. The main input arguments of the subroutine include $u$ (wind speed), $T$ (air temperature), $T_s$ (water temperature), $q$ (specific humidity), $R_{li}$ (downward shortwave radiation), $R_{si}$ (downward longwave radiation), and $r$ (rain rate). The output covers $\tau$ (wind stress), $H_s$ (sensible heat) flux, $H_l$ (latent heat flux), $L_e$ (latent heat of evaporation) and many other parameters. During the simulation, sensible heat flux and latent heat flux, calculated by COARE using bulk formulae, are used to estimate the total water surface heat exchange. To provide compatibility with the EFDC+ hydrodynamics module, the wind stress value is not used directly. Instead, the wind drag coefficient estimated by COARE is used to calculate the two horizontal components of surface wind stress. The evaporation rate is also used as part of boundary conditions.

EFDC+ Explorer Graphical User Interface

The EFDC+ Explorer graphic user interface has been updated to provide COARE 3.6 as an option for calculating water surface heat exchange. Figure 1 shows the setup of the COARE 3.6 option for surface heat exchange. The parameters include PBL height, which is set to as the default value, the height of the temperature/humidity sensor used for measurement, and the number of iterations of the COARE algorithm.

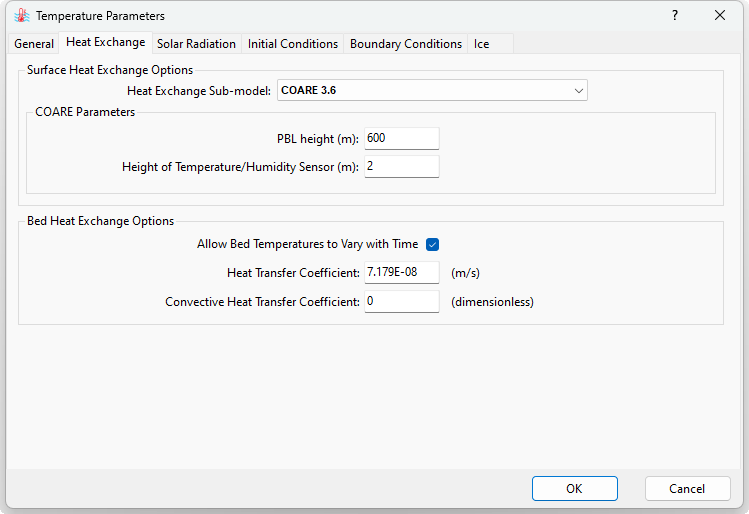
Users should note that when the COARE option is selected, the evaporation option will be switched directly to the COARE method, as shown in Figure 2.

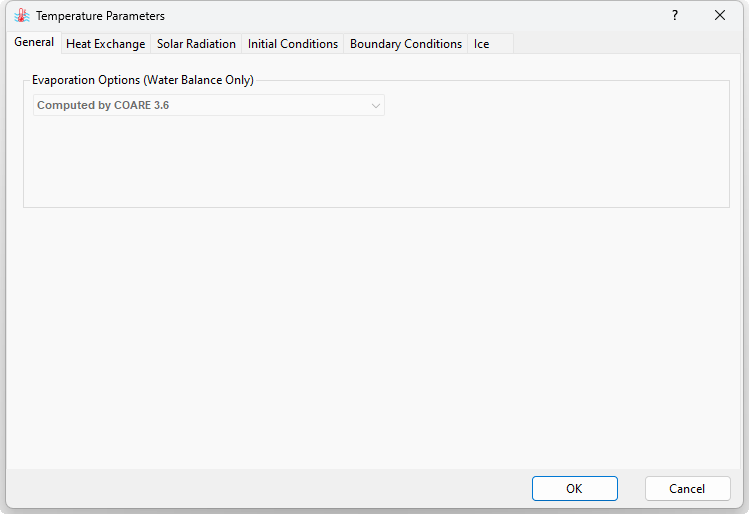
Conclusion

COARE has been successfully implemented in EEMS and will be part of the upcoming EEMS 12.1 release. Look out for a future blog post, where we will compare the results for the various heat options now available in EEMS and offer suggestions as to which option should be used in which application.

Talk To The Experts

Paul Craig, PE

President and Senior Consultant

Tran Duc Kien, Ph.D.

Water Resources Engineer